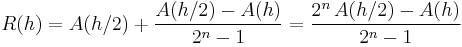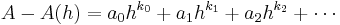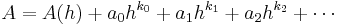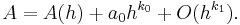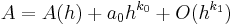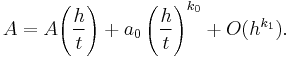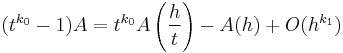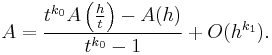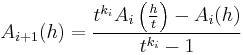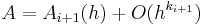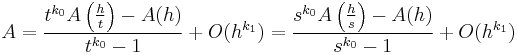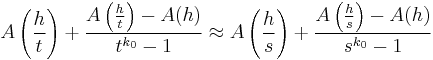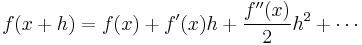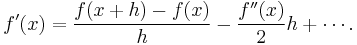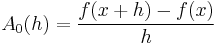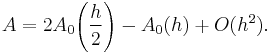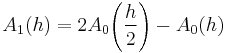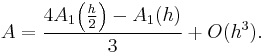Richardson extrapolation

In numerical analysis, Richardson extrapolation is a sequence acceleration method, used to improve the rate of convergence of a sequence. It is named after Lewis Fry Richardson, who introduced the technique in the early 20th century.[1][2] In the words of Birkhoff and Rota, "... its usefulness for practical computations can hardly be overestimated."[3]

Practical applications of Richardson extrapolation include Romberg integration, which applies Richardson extrapolation to the trapezium rule, and the Bulirsch–Stoer algorithm for solving ordinary differential equations.

Contents

Example of Richardson extrapolation

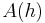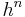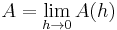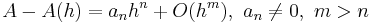Suppose that A(h)\; is an estimation of order h^n\; for A=\lim_{h\to 0}A(h), i.e. A-A(h) = a_n h^n%2BO(h^m),~a_n\ne0,~m>n. Then

R(h) = A(h/2) %2B \frac{A(h/2)-A(h)}{2^n-1} = \frac{2^n\,A(h/2)-A(h)}{2^n-1}

is called the Richardson extrapolate of A(h); it is an estimate of order hm for A, with m>n.

More generally, the factor 2 can be replaced by any other factor, as shown below.

Very often, it is much easier to obtain a given precision by using R(h) rather than A(h') with a much smaller h' , which can cause problems due to limited precision (rounding errors) and/or due to the increasing number of calculations needed (see examples below).

General formula

Let A(h) be an approximation of A that depends on a positive step size h with an error formula of the form

A - A(h) = a_0h^{k_0} %2B a_1h^{k_1} %2B a_2h^{k_2} %2B \cdots

where the ai are unknown constants and the ki are known constants such that hki > hki+1.

The exact value sought can be given by

A = A(h) %2B a_0h^{k_0} %2B a_1h^{k_1} %2B a_2h^{k_2} %2B \cdots

which can be simplified with Big O notation to be

A = A(h)%2B a_0h^{k_0} %2B O(h^{k_1}). \,\!

Using the step sizes h and h / t for some t, the two formulas for A are:

A = A(h)%2B a_0h^{k_0} %2B O(h^{k_1}) \,\!
A = A\!\left(\frac{h}{t}\right) %2B a_0\left(\frac{h}{t}\right)^{k_0} %2B O(h^{k_1}) .

Multiplying the second equation by tk0 and subtracting the first equation gives

(t^{k_0}-1)A = t^{k_0}A\left(\frac{h}{t}\right) - A(h) %2B O(h^{k_1})

which can be solved for A to give

A = \frac{t^{k_0}A\left(\frac{h}{t}\right) - A(h)}{t^{k_0}-1} %2B O(h^{k_1}) .

By this process, we have achieved a better approximation of A by subtracting the largest term in the error which was O(hk0). This process can be repeated to remove more error terms to get even better approximations.

A general recurrence relation can be defined for the approximations by

A_{i%2B1}(h) = \frac{t^{k_i}A_i\left(\frac{h}{t}\right) - A_i(h)}{t^{k_i}-1}

such that

A = A_{i%2B1}(h) %2B O(h^{k_{i%2B1}})

with A_0=A(h).

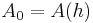The Richardson extrapolation can be considered as a linear sequence transformation.

Additionally, the general formula can be used to estimate k0 when neither its value nor A is known a priori. Such a technique can be useful for quantifying an unknown rate of convergence. Given approximations of A from three distinct step sizes h, h / t, and h / s, the exact relationship

A=\frac{t^{k_0}A\left(\frac{h}{t}\right) - A(h)}{t^{k_0}-1} %2B O(h^{k_1}) = \frac{s^{k_0}A\left(\frac{h}{s}\right) - A(h)}{s^{k_0}-1} %2B O(h^{k_1})

yields an approximate relationship

A\left(\frac{h}{t}\right) %2B \frac{A\left(\frac{h}{t}\right) - A(h)}{t^{k_0}-1} \approx A\left(\frac{h}{s}\right) %2B\frac{A\left(\frac{h}{s}\right) - A(h)}{s^{k_0}-1}

which can be solved numerically to estimate k0.

Example

Using Taylor's theorem,

f(x%2Bh) = f(x) %2B f'(x)h %2B \frac{f''(x)}{2}h^2 %2B \cdots

the derivative of f(x) is given by

f'(x) = \frac{f(x%2Bh) - f(x)}{h} - \frac{f''(x)}{2}h %2B \cdots.

If the initial approximations of the derivative are chosen to be

A_0(h) = \frac{f(x%2Bh) - f(x)}{h}

then ki = i+1.

For t = 2, the first formula extrapolated for A would be

A = 2A_0\!\left(\frac{h}{2}\right) - A_0(h) %2B O(h^2) .

For the new approximation

A_1(h) = 2A_0\!\left(\frac{h}{2}\right) - A_0(h)

we can extrapolate again to obtain

A = \frac{4A_1\!\left(\frac{h}{2}\right) - A_1(h)}{3} %2B O(h^3) .

See also

References

  1. ^ Richardson, L. F. (1911). "The approximate arithmetical solution by finite differences of physical problems including differential equations, with an application to the stresses in a masonry dam". Philosophical Transactions of the Royal Society of London, Series A 210 (459-470): 307–357. doi:10.1098/rsta.1911.0009. 
  2. ^ Richardson, L. F.; Gaunt, J. A. (1927). "The deferred approach to the limit". Philosophical Transactions of the Royal Society of London, Series A 226 (636-646): 299–349. doi:10.1098/rsta.1927.0008. 
  3. ^ Page 126 of Birkhoff, Garrett; Gian-Carlo Rota (1978). Ordinary differential equations (3rd ed.). John Wiley and sons. ISBN 047107411X. OCLC 4379402. 

External links